Welcome to AP Physics SPRING SEMESTER!
Click here to jump to current week.
Week 1: Jan 06, 2025
- Feel the Torque! This lab had students placing weights at various points on a meter stick and then holding the stick at predefined angles in order to calculate and feel the torque.
- Determination of Max Omega! This lab had students sitting on the “Sit and Spin” chair and simply measuring the maximum rotational velocity in RPM and Rad/sec.
Week 2: Jan. 13, 2025
- Feel the Moment (of Inertia). Students considered the acceleration of an ordinary hammer about three different axis. For each axis, students were to consider the hammer (the handle and the ‘head’) as the Sum of geometric objects, each with its own, Moment of Inertia. The students are to both draw the shapes individually, and showing what the equation of Moment of Inertia is for each, and then show how the total Moment of Inertia is the ‘sum of the parts’.
- Video: Johannes Kepler While Clark was out, students were to watch and take notes this short (30 min.) documentary on Kepler’s life and accomplishments. Students should focus their attention on how his upbringing, how he survived, the role that Tycho Brahe played in his life and his theories of planetary motion. What are the three Laws of motion which he finally determined?
- Homework set: Problems 1, 5, 7, 8 on page 275 and problems 3, 7, 8, 11 on pages 460-461 of the on-line text book.
Week 3: Jan. 20, 2025
- Model Moment of Inertia lab. This lab had students attempting to model the moment of inertia of a system consisting of an aluminum plate with three masses located asymetricaly on top (one of which was a force/accelerometer). They applied a known torque to the system, measured the subsequent rotational acceleration and from that, deduced what the ‘measured’ Moment of Inertia must be for the system.
- rewrite: Why doesn’t the spinning wheel fall? Students were to ‘give back’ the lecture and demonstrations that Clark gave showing how ‘vector math’ predicts the solution of the wheel precessing about a new center-line. This Wikipedia page describes in detail, the torques which lead to precession.

Week 4: Jan. 27, 2025
- Podcast: The Science of Friction. Students were to take a page of notes, highlighting the factors that affect friction, how we measure it, etc.
- On-line Practice Ap Test. Students should see how well they do in this test and we’ll discuss next week. (note: The students need to log into the AP Classroom website to take the test. They MAY work together to discuss).
As an exciting example of the Universe at Work.. we explored the world of Pulsars, Neutron Stars and Magnetars and how Conservation fo Angular Momentum is conserved and leads to objects which spin at hundreds of times per second, but contain the mass of hundreds of Suns
With that in mind, the concept of Angular momentum and the conservation thereof, was introduced. For demonstration, Clark brought out a rotating platform/stool, and demonstrated how holding a spinning bike-wheel in different orientations resulted in the ‘system as a whole’ responding. Also, introduced, was the concept of using vectors to represent roational values (omega as the rotational velocity and L as the momentum vector.. L = I omega).
On Thursday, we stepped into the demonstration of the wheel being spun up and then being suspended by the end of axel rod. Clark then walked through the vector physics predicting the observed motion centered on the idea that ‘if you can see the direction of the forces/torque, you can also see the direction fo the change in velocity/omega). Students were tasked with taking notes during the lecture and then rewriting them such that they look like a college text book section on the matter.
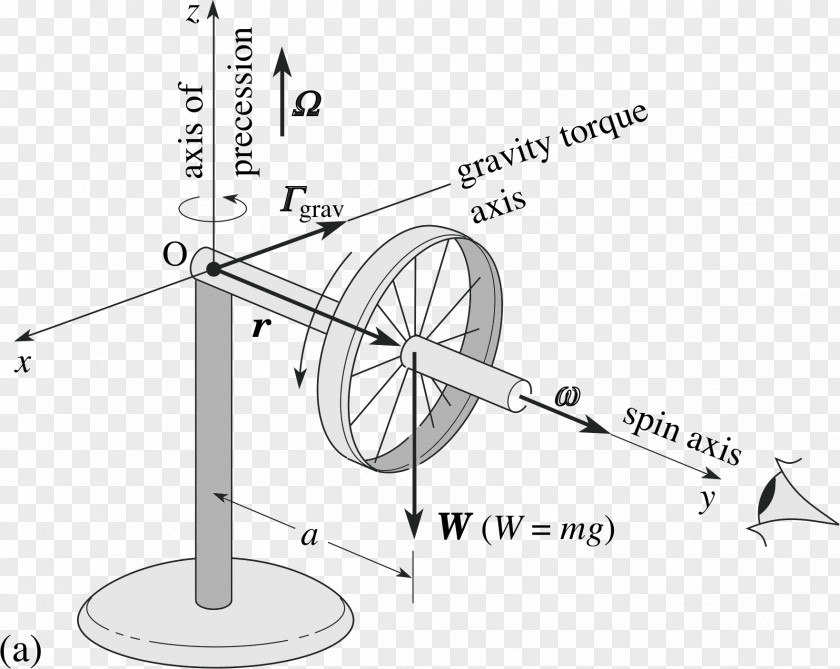
Week 5: Feb. 03, 2025
- Introduction of Kinetic Energy of a rotating system and how we can use conservation of energy principals to rotating systems. Specifically we considered a disk rolling down a ramp and how the gravitational potential energy would be distributed between the rotational kinetic energy and the linear (translational) kinetic energy.
- A special emphasis was placed on how to link linear motion (of a bucket falling) to rotational motion (of the pulley supporting the bucket).
- Text book problems (page 461) 13, 15, 20, 22, 27, 32, 39.
- chpt 10_rotational dynamics and energy
The main ‘new’ discussion was examining a problem in which a bucket suspended from a rope wrapped around a pully will descend by using the transformation from tangential velocity to rotational velocity to ‘tie’ the two components of the problem together.. Also discussed, was how we can use concepts of energy to determine the rotational velocity and linear velocity of a disk rolling down an incline plane.

Week 6: Feb. 10, 2025
Week 7: Feb. 17, 2025
No School! Ski Week!
Week 8: Feb. 24, 2025
- A quick review of Power = work/time (joules/sec = Watts or Horse Power)
- Nelson Racing Engines main website
- NRE 2500 HP dyno test
- GM Performance Parts Crate Engines page (632 c.. = 1000 HP!)
- Test 1:(Spring) Rotational Dynamics
- Particle Fever (video) Students took a page of notes on the development of the Large Hadron Collide
Week 9: March. 03, 2025
- Article: Probing the Proton. Students annotated this article. (A good follow up to the video: Particle Fever).
Week 10: March. 10, 2025
- Restoring forces
- Spring Constant
- Conservation of Energy in an oscillating system
- oscillating systems. This lab made use of Smart Cars on incl
Also discussed was the list of topics students should be familiar with for Friday’s practice AP Test on Rotational Dynamics. Students were encouraged to review Unit-7-AP-Physics-1

Week 11: March. 17, 2025
- Putting theory to practice; namely taking the ‘text book’ problem of a mass and spring system, we set up our own to see for ourselves.
- Share a problem. The idea with this activity, is that each day, students will take turns sharing with the class, a particular physics problem which at first stumped them and then they figured out. Clark will maintain a calendar of students presentation dates.
Also discussed was the list of topics students should be familiar with for Friday’s practice AP Test on Rotational Dynamics. Students were encouraged to review Unit-7-AP-Physics-1
Thursday’s class centered on Clark’s own lab experiment (oscillating systems) and the conversation of how each energy system requires its own version of the position data. (ie., to calculate energy stored in the spring, the position data set places the zero mark at the top whereas for calculations of gravitational potential energy, the zero mark needs to be at the bottom).
Week 12: March. 24, 2025
- Wave speed is ‘fixed’ (for a given substance)
- Waves can pass through each other without interacting
- Waves can ‘interfere’ with each other in the substance
- Waves can reflect
- Introduction to harmonics (the series of frequencies and wave forms which can exist in a system).
- slinky waves_spring 25
- Waves on a string simulator. (student handout: waves on a string)
Friday students spent time on the practice AP test for oscillations.

Student Project showing Computational Fluid Dynamics of Vortex shedding.
Of special Interest: This video explores the latest, state-of-the-art machines doing Laser Photolithography to manufacture semiconductors.
Week 13: March. 31, 2025
- Considering how wave harmonics can exist in air (sound).. and using fixed frequency tuning forks to determine the speed of sound
- Predicting wave forms in a cylinder ‘open at one end’
- Introduction to music as a function of wavelength and harmonic number.
Week 14: April 07, 2025 Ski Week!
Week 15: April 14, 2025
- Introduction to Pressure.
- Triple point of water.
- The formation of ‘shock waves’ as aircraft reach the speed of sound
- Buoyancy
- Buoyancy lab. Students were given a wooden dowel and then tasked with first determining the density of the piece, then based on principals of buoyancy the students were to determine what fraction of the dowel would remain above water (note: meaning how many cm would remain above water). Students did this math individually including a drawing the system, all measured values and math along the way. (percent error too!). For Extra Credit, students also determined the uncertainty in the measurements and the percent uncertainty in their final value).
- (note: concrete canoes are a standard engineering project at university)
- FRQ: 1 + 2 from Unit 7: Oscillations. (students were to download the on-line Blue Book and use the secure web browser for this test today)
A quick demonstration was done after bringing up the Digital Dutch webpage showing that 1 Atm. = 14.6 lbs/square inch. What does this mean? After filling up an Erlymeyer flask with water, and noting that the opening is roughly 2.5 square inches… means that the total force on the opening is roughly 38 lbs of force total. Clark then turned the flask upside down with nothing more than a piece of cardstock to close it up.

The triple point of water was introduced to illustrate the effects of different pressures on the state of water. Doppler effect and shock waves..
This then was seen first hand when a fighter jet passes by spectators during SF Fleet Week.
Week 16: April 21, 2025
- Introduction to fluids in motion (fluid dynamics) and comparisons between Fluid Statics and Fluid Dynamics.
- Bernoulli’s Equations:
- (note: concrete canoes are a standard engineering project at university)
- FRQ: 1 + 2 from Unit 7: Oscillations. (students were to download the on-line Blue Book and use the secure web browser for this test today)
Week 17: April 28, 2025
- Bernoulli’s equations (for fluid dynamics.. i.e., fluids in motion)
New Assignments:
- Chpt 11 problems: 5, 10, 11, 12, 25. (page 514 of text). (solutions to chpt 11 hw set (5, 10, 11, 12, 25)
- Video: Breaking the sound barrier. Students were to take a page of notes.
- Students took the AP Classroom, practice AP Test for Fluids today (both multiple choice and FRQ’s)
Video: Breaking the sound barrier. This Modern Marvels documentary describes the engineering challenges of trying to create a plane that could fly faster than sound and more importantly, be controllable. Chuck Yeager emerges as the hero of the day. Students were to take a page of notes.
Discussion: Bernoulli’s’ equations for fluids in motion. First we watched this video which is a great introduction to Bernoulli’s principals.
Week 17: April 28, 2025
- Bernoulli’s equations (for fluid dynamics.. i.e., fluids in motion)
New Assignments:
- Chpt 11 problems: 5, 10, 11, 12, 25. (page 514 of text). (solutions to chpt 11 hw set (5, 10, 11, 12, 25)
- Video: Breaking the sound barrier. Students were to take a page of notes.
- Students took the AP Classroom, practice AP Test for Fluids today (both multiple choice and FRQ’s)
Video: Breaking the sound barrier. This Modern Marvels documentary describes the engineering challenges of trying to create a plane that could fly faster than sound and more importantly, be controllable. Chuck Yeager emerges as the hero of the day. Students were to take a page of notes.
Discussion: Bernoulli’s’ equations for fluids in motion. First we watched this video which is a great introduction to Bernoulli’s principals.


